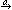 if a process can perform event a when in state I, and
I refuses X if it may refuse set X in that state.
If state I diverges, then we write
I
if a process can perform event a when in state I, and
I refuses X if it may refuse set X in that state.
If state I diverges, then we write
I .
.
For the mathematically minded, the principle underlying the proof method is a form of fixed-point induction. For the underlying theory, see [Roscoe91].
We write
I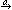 if a process can perform event a when in state I, and
I refuses X if it may refuse set X in that state.
If state I diverges, then we write
I
if a process can perform event a when in state I, and
I refuses X if it may refuse set X in that state.
If state I diverges, then we write
I .
.
Mathematically, the abstraction function into the denotational model combines the information from the set of all states reachable on a given trace to determine the corresponding observable behaviour.
Although it is not formally compliant with these standards.
It thus provides the same user interface function as the FDR1 interface.
Occasionally, process constructs may arise in which a single syntactic subcomponent has more than one independent contribution to the behaviour being examined. In this case one branch will be created for each contribution.
The resulting set must actually be rectangular (see A.3.3 Datatypes).
Of course, this COUNT(n) is a finite process only if n is between 0 and N...
Again, this is not strictly true, as FDR2 has the capability to check refinements involving some kinds of infinite processes. In particular, infinite specifications such as "is a buffer" have been used experimentally in FDR2, but the compiler does not yet support such features.
And which incidentally has 2 1024 [2 to the power 1024] states, which it would not be wise to try and explore directly; applying a compression such as normalise to the "else" branch makes such constructs entirely reasonable, however.
The idea of a normal form for CSP processes has its origins in [Brookes83], where it is shown that each finite CSP term is equivalent to one in a particular normal form.
The classic dining philosophers example has N Chinese philosophers sat at a round table, with a chopstick between each philosopher (so, there are N chopsticks). After some thinking a philosopher will become hungry and want to eat some rice. To do this he must pick up the chopstick on his left, then the one on his right. If they all become hungry at once, no philosopher will get a right chopstick, so they will starve.
It is possible to draw finer distinctions within "true", for instance to explore notions of fairness and inevitability of divergence.
The convention is that T is the set of nodes of the GTLS T.
The renaming operators replace both the functional and inverse-functional renaming operations of [Hoare85]. Identifiers not targeted in a renaming are left alone.
This document was generated on 23 November 1998 using the texi2html translator version 1.51.