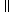Q)
used by Hoare, we employ an operator parameterised by the interface sets
of the components: in
The CSP notation, of which we have seen a number of examples so far, developed as a collection of algebraic operators denoting various ways of building and combining processes. To apply an automated tool to CSP definitions we need a way of entering them into computers: CSP needs to become more like a programming language. The most important decisions that have to be taken in doing this are not so much how to represent the operators in machine-readable form, but less obvious issues such as the collection of data-types to be supported for values passed over channels and as the state of processes, and the way a program and definitions are structured.
A proposed standard has been developed at Oxford under an ONR-funded project. The full language is described in A Syntax Reference.
The only significant difference from the version of CSP in Hoare's book
is in the treatment of alphabets and how these affect parallel
composition.
In the modern treatment, processes do not have intrinsic alphabets as in
Hoare's book.
This requires us to specify the interface between processes operating in
parallel explicitly.
Rather than the single synchronised parallel composition operator
(P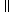Q)
used by Hoare, we employ an operator parameterised by the interface sets
of the components: in
PQ
(expressed in the machine-readable language as P[X||Y]Q),
P is constrained to perform only events in X, Q
performs events from Y, and events in the intersection
X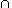
Y
are synchronised.
A useful alternative is to specify a set of synchronised events and
allow events outside this set to be interleaved.
Where this interface set of synchronised events is X, we write
this as
PQ
(expressed in linear form as P[|X|]Q).
This form of parallel composition makes many definitions more concise,
and is the one generally used in the example files.
The reference to the language of process definitions interpreted by FDR can be found in A Syntax Reference. The remainder of this section describes the practical usage of the language. Larger examples of how the syntax works, and of various styles that can be useful in designing CSP processes, may be found in the supplied examples in the `demo' directory.
Processes are described by giving the checker a series of equational definitions, in the usual CSP style. An input file to FDR may consist of a series of such definitions, plus additional information about the environment in which the definitions should be interpreted. To assist in making descriptions comprehensible, comments may be included: a double-dash (`--') and any subsequent text on the line are ignored if they occur in either of the following positions:
Line breaks can also occur at either of the above positions. To facilitate structuring and re-use of definitions, system descriptions can be split across files. The command
include "myfile.csp"
causes the text of the specified file (`myfile.csp' in this case)
to be read in as if it had been physically included at the point where
the include command occurs.
Such included files can be nested.
In order to interpret communication events, FDR must be provided
with some information which is often expressed informally in written CSP
documents.
In particular, the set of possible communications events must be
defined, including the sets of possible values communicated on each
referenced channel.
Events or channels are declared by the keyword channel.
Thus, we might write:
channel c1,c2 : {v1,v2,v3,v4}
V = {v1,v2,v3,v4}
channel d1,d2 : V
The first defines channels c1 and c2 which can communicate
values from the set v1,..., while the second is equivalent,
except that the type is described by a name, previously defined as a set
of values.
FDR2 actually allows almost(7) arbitrary set expressions after the colon:
channel decrease : { i.j | i<-{1,2,3}, j<-{1,2} }
Other data-types can be declared by a datatype clause:
datatype V = v1 | v2 | v3 | v4
channel c1,c2 : {v1,v2,v3,v4}
channel d1,d2 : V
To declare a simple event, rather than a channel passing values, we simply omit the type term:
channel e1,e2,e3
To allow the use of more complex CSP communication constructs, we can declare dotted compound events, for example after a declaration
NUMBERS = {0,1,2,3}
datatype X = a | b | c | d
channel xxx : NUMBERS . {a,b,c}
the output xxx.1!b and the input xxx.i?v (where i
is in {0,1,2,3} are valid event descriptions.
In FDR1, the order of these declarations could be significant; in FDR2 this restriction is relaxed, but "declaration before use" is probably a reasonable style to adopt in any case.
In FDR2, genuine functions can be declared and used freely:
square(n) = n * n P = in ? x -> out ! square(x) -> P
Process definitions can use parameters to represent internal state. For example, a counter whose values are bounded by 0 and N may be described:(8)
COUNT(n) = n!=0 & down -> COUNT(n-1)
[] n!=N & up -> COUNT(n+1)
The parameter n represents the internal state of the process.
To be able to explore such processes mechanically, we must be able to
enumerate their states (although this is not strictly true in the full
generality of FDR2).
Thus an unbounded counter, which has an infinite state space, could not
be checked by FDR, and indeed attempting to use such a definition
may cause FDR to enter an endless loop.(9)
The data-types which can be used as process parameters include truth
values, integers and also sets and sequences of such values.
Because interfaces are usually defined in terms of channels, not
individual events, a special notation is provided for writing event
sets: the notation {|a,b,c|} expands to a set of events when
a, b, c are either individual events or
channels.
The set of all possible communications along a channel is substituted
for the channel name in the latter case.
Thus, if we declare
channel a : {0,1,2}
channel b : {open, close}
channel d
we have
{| a,b,d |} == {a.0, a.1, a.2, b.open, b.close, d}
FDR also supports unsynchronised parallel composition
(P|||Q), hiding (P\A), renaming (P[[a<-b]]) and
`linked parallel' (P[out<->in]Q).
These operators and the manner in which they may be used are discussed
in A.4 Processes.
Any process structure which is allowed in FDR1 is valid in FDR2. The latter, however, relaxes the former's "high/low level" distinction in two significant ways:
defines Q to be a process which can do 1024 a's before stopping.(10)channel a P(n) = if n == 0 then a -> STOP else P(n-1) ||| P(n-1) Q = P(10)
channel a,b,c,d,e P = (a -> b -> SKIP ||| c -> d -> SKIP); e -> P
One form of operator available in FDR2, but additional to those offered by earlier versions, is the transparent function. These are typically used for compression functions, such as those described in 5.1 Using Compressions. According to the philosophy of [Scat95], their gross semantic effect should be that of the identity function, since any tool which does not recognise them is entitled to ignore them; but they may dramatically affect the way in which those semantics are realised operationally. The range of functions supported in this way is determined at link-time of the refinement engine, and thus may be extended; those currently supported are described in 5.1 Using Compressions.
In order to use a transparent function, it must be made known to the
parser using the transparent keyword, and may then be applied to
any process term:
transparent diamond ... etc ... P = Q [| A |] diamond((R [| B |] S) \ B)
The following section gives a sample script for FDR2.
Go to the Next or Previous section, the Detailed Contents, or the FS(E)L Home Page.