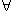 a
a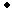 (I
(I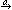 )
)
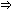 (S
(S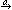 )
)
For processes which can only mutually reach a finite number of distinct pairs of states, we may check that a refinement relation holds between them by a process of induction.(1) The basic strategy is as follows: suppose we consider any corresponding states S of specification Q and I of implementation P. The conditions which any such pair must satisfy if failures-divergences refinement is to hold are that any event which is immediately possible for the implementation must be possible for the specification:(2)
a
(I
)
(S
)
Any refusal of I is allowable for S:
X
(I refuses X)
(S refuses X)
And divergence is only possible for I if it is for S:
I
S

Because any subset of a set which can be refused is also a refusal, it is sufficient to test that each maximal refusal of I is included in a refusal of S.
Having checked that a particular pair is correct, it is then necessary to check that all pairs reachable from this one are, and so on. Refinement is established once all the pairs that are reachable have been checked (i.e., all the new states are ones that have already been seen).
In general, simply exploring the cross-product of the state-spaces in this way does not work: just because it is possible for the specification to reach a state which appears to exclude a given behaviour of the implementation, it is not necessarily the case that there is not another possible state of the specification machine which would permit it.(3) In order to avoid this possibility, FDR requires -- and ensures -- that the specification process be reduced to a normal form, with at most one state reachable on any trace; in practice, this means that all internal transitions are eliminated and that there is at most one transition from any state by any given event. The algorithm to achieve this produces states in the normalised machine corresponding to sets of states in the unnormalised specification; in theory (and in some pathological cases) this may make the normal form exponentially larger than the original, but in most real examples normalisation in fact reduces the state-space, often dramatically.
FDR is designed to mechanise the process of carrying out refinement checks. For a wide class of CSP processes, it is possible to expand the state space of the process mechanically, and perform the tests above using a standard search strategy.
Go to the Next or Previous section, the Detailed Contents, or the FS(E)L Home Page.