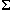5.1.4 Hiding and deadlock

In the stable failures model, a system P can deadlock if and only if P \ 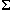can. In other words, we can hide absolutely all events -- and move this hiding as far into the process as possible using the principles already discussed.

Consider the case of the N dining philosophers (in a version, for simplicity, without a Butler process).(12) A way of building this system up hierarchically is as progressively longer chains of the form

PHIL₀ FORK₀ PHIL₁ ... FORK_i-1 PHIL_i

In analysing the whole system for deadlock, we can hide all those events of a subsystem that do not synchronise with any process outside the subsystem. Thus, in this case we can hide all events other than the interactions between PHIL₀ and FORK_N-1, and between PHIL_m and FORK_m. The failures normal form of the subsystem will have very few states (exactly 4). Thus, we can compute the failures normal form of the whole hidden system, adding a small fixed number of philosopher/fork combinations at a time, in time proportional to N, even though an explicit model-checker would find exponentially many states.

We can, in fact, do even better than this. Imagine doing the following:

• First, build a single philosopher/fork combination hiding all events not in its external interface, and compress it. This will (with standard definitions) have 4 states.
• Next, put, say, 10 copies of this process together in parallel, after suitable renaming, to make them into consecutive pairs in a chain of philosophers and forks (the result will have approximately 4000 states). Compress this to its 4 states.
• Now, in the same way, rename this process in 10 different ways so that it looks like 10 adjacent groups of philosophers, compute the results and compress it.
• And repeat this process as often as you like... Clearly it will take time linear in the number of times you do it.

By this method we can produce a model of 10 ^N [10 to the power N] philosophers and forks in a row in time proportional to N. To make them into a ring, all you would have to do would be to add another row of one or more philosophers and forks in parallel, synchronising the two at both ends. Depending on how it was built (such as whether all the philosophers are allowed to act with a single-handedness) you would either find deadlock or prove it absent from a system with doubly exponential number of states.

This example is, of course, extraordinarily well-suited to our methods. What makes it work are firstly the fact that the networks we build up have a constant-sized external interface (which could only happen in networks that were, like this one, chains or nearly so) and have a behaviour that compresses to a bounded size as the network grows.

On the whole we do not have to prove deadlock freedom of quite such absurdly large systems. We expect that our methods will also bring great improvements to the deadlock checking of more usual size ones that are not necessarily as perfectly suited to them as the example above.

Go to the Next or Previous section, the Detailed Contents, or the FS(E)L Home Page.