 actions and each node has at most one successor under each
a
actions and each node has at most one successor under each
a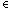
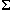
We mentioned earlier that one of the advances this second-generation version of FDR offers is the ability to build up a system gradually, at each stage compressing the subsystems to find an equivalent process with (hopefully) many less states. This is one of the ways (and the only one which is expected to be released in the immediate future) in which implicit model-checking capabilities have been added to FDR.
By these means we can certainly rival the sizes of systems analysed by BDD's (see [Clarke90], for example), though like the latter, our implicit methods will certainly be sensitive to what example they are applied to and how skillfully they are used. Hopefully the examples later in these sections will illustrate this.
The idea of compressing systems as they are constructed is not new, and indeed it has been used to a very limited extent in FDR for several years (bisimulation is used to compact the leaf processes). What is new is that the nature of CSP equivalences is exploited to achieve far better compressions in some cases than can be achieved using other, stronger equivalences.
These sections summarise the main compression techniques implemented so far in the FDR2 refinement engine and give some indications of their efficiency and applicability. Further details can be found in [RosEtAl95].
The concept of a Generalised Labelled Transition System (GLTS) combines
the features of a standard labelled transition system and those of the
normal-form transition systems used in FDR1 to represent
specification processes [Roscoe94].
Those normalised machines are (apart from the nondeterminism coded in
the labellings) deterministic in that there are no
 actions and each node has at most one successor under each
a
actions and each node has at most one successor under each
a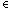
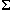
The structures of a GLTS allow us to combine the behaviour of all the
nodes reachable from a single P under
 actions into one node:
actions into one node:
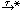 Q.
Q.
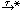 Q.
Q.
 -path
(invariably containing a loop, in a finite graph) from P.
-path
(invariably containing a loop, in a finite graph) from P.
 actions.
actions.
Two things should be pointed out immediately:
 -free
GLTS, but one which probably has as many (and more complex) nodes than
the old one.
Just because
P
-free
GLTS, but one which probably has as many (and more complex) nodes than
the old one.
Just because
P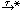 Q.
and Q's behaviour has been included in the compressed version of
P, this does not mean we can avoid including a compressed version
of Q as well: there may well be a visible transition that leads
directly to Q.
One of the main strategies discussed below -- diamond elimination --
is designed to analyse which of these Q's can, in fact, be
avoided.
Q.
and Q's behaviour has been included in the compressed version of
P, this does not mean we can avoid including a compressed version
of Q as well: there may well be a visible transition that leads
directly to Q.
One of the main strategies discussed below -- diamond elimination --
is designed to analyse which of these Q's can, in fact, be
avoided.
FDR2 is designed to be highly flexible about what sort of transition systems it can work on. We will assume, however, that it is always working with GLTS ones which essentially generalise them all. The operational semantics of CSP have to be extended to deal with the labellings on nodes: it is straightforward to construct the rules that allow us to infer the labelling on a combination of nodes (under some CSP construct) from the labellings on the individual ones.
Go to the Next or Previous section, the Detailed Contents, or the FS(E)L Home Page.