 -reachibility
is a partial order on nodes.
If the input transition system is known to be divergence free then this
is true, otherwise
-reachibility
is a partial order on nodes.
If the input transition system is known to be divergence free then this
is true, otherwise
 -loop
elimination is required first (since this procedure guarantees to
achieve the desired state).
-loop
elimination is required first (since this procedure guarantees to
achieve the desired state).
This procedure assumes that the relation of
 -reachibility
is a partial order on nodes.
If the input transition system is known to be divergence free then this
is true, otherwise
-reachibility
is a partial order on nodes.
If the input transition system is known to be divergence free then this
is true, otherwise
 -loop
elimination is required first (since this procedure guarantees to
achieve the desired state).
-loop
elimination is required first (since this procedure guarantees to
achieve the desired state).
Under this assumption, diamond reduction can be described as follows, where the input state-machine is S (in which nodes can be marked with information such as minimal acceptances), and we are creating a new state-machine T from all nodes explored in the search:
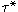 (N)
of all nodes reachable from N under a (possibly empty) sequence
of
(N)
of all nodes reachable from N under a (possibly empty) sequence
of
 actions.
actions.
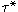 (N)
is either marked as divergent or has a
(N)
is either marked as divergent or has a
 to itself.
The minimal acceptances are the union of those of the members of
to itself.
The minimal acceptances are the union of those of the members of
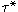 (N)
with non-minimal sets removed.
This information is used to mark N in T.
(N)
with non-minimal sets removed.
This information is used to mark N in T.
 actions possible for any member of
actions possible for any member of
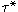 (N).
(N).
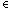 V(N),
the set
Na = N after a
of all nodes reachable under a from any member of
V(N),
the set
Na = N after a
of all nodes reachable under a from any member of
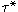 (N).
(N).
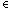 V(N), the set
min(Na) which is the set of all
V(N), the set
min(Na) which is the set of all
 -minimal elements of
Na (i.e., those nodes not reachable under
-minimal elements of
Na (i.e., those nodes not reachable under
 from any other in
Na).
from any other in
Na).
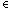 V(N).
Any nodes not already explored are added to the search.
V(N).
Any nodes not already explored are added to the search.
This creates a transition system where there are no
 -actions
but where there can be ambiguous branching under visible actions, and
where nodes might be labelled as divergent.
The reason why this compresses is that we do not include in the search
nodes where there is another node similarly reachable but demonstrably
at least as nondeterministic: for if
M
-actions
but where there can be ambiguous branching under visible actions, and
where nodes might be labelled as divergent.
The reason why this compresses is that we do not include in the search
nodes where there is another node similarly reachable but demonstrably
at least as nondeterministic: for if
M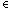
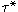 (N)
then N is always at least as nondeterministic as M.
The hope is that the completed search will tend to include only those
nodes that are
(N)
then N is always at least as nondeterministic as M.
The hope is that the completed search will tend to include only those
nodes that are
 -minimal in
T.
Notice that the behaviours of the nodes not included from
Na
are nevertheless taken account of, since their divergences and minimal
acceptances are included when some node of
min(Na)
is explored.
-minimal in
T.
Notice that the behaviours of the nodes not included from
Na
are nevertheless taken account of, since their divergences and minimal
acceptances are included when some node of
min(Na)
is explored.
It seems counter-intuitive that we should work hard not to unwind
 's
rather than doing so eagerly.
The reason why we cannot simply unwind
's
rather than doing so eagerly.
The reason why we cannot simply unwind
 's
as far as possible (i.e., collecting the
's
as far as possible (i.e., collecting the
 -maximal
points reachable under a given action) is that there will probably be
visible actions possible from the unstable nodes we are trying to
bypass.
It is impossible to guarantee that these actions can be ignored.
-maximal
points reachable under a given action) is that there will probably be
visible actions possible from the unstable nodes we are trying to
bypass.
It is impossible to guarantee that these actions can be ignored.
The reason we have called this compression diamond elimination is
because what it does is to (attempt to) remove nodes based on the
diamond-shaped transition arrangement where we have four nodes
P, P', Q, Q' and
P  P',
Q
P',
Q  Q',
P
Q',
P 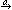 Q and
P'
Q and
P' 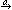 Q'.
Starting from P, diamond elimination will seek to remove the
nodes P' and Q'.
The only way in which this might fail is if some further node in the
search forces one or both to be considered.
Q'.
Starting from P, diamond elimination will seek to remove the
nodes P' and Q'.
The only way in which this might fail is if some further node in the
search forces one or both to be considered.
A Lemma in [RosEtAl95] shows that the following two types of node are certain to be included in T:
 -minimal
nodes (ones not reachable under
-minimal
nodes (ones not reachable under
 from any other).
from any other).
Let us call
S0
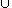 {N0}
the core of S.
The obvious criteria for judging whether to try diamond reduction at
all, and of how successful it has been once tried, will be based on the
core.
For since the only nodes we can hope to get rid of are the complement of
the core, we might decide not to bother if there are not enough of these
as a proportion of the whole.
And after carrying out the reduction, we can give a success rating in
terms of the percentage of non-core nodes eliminated.
{N0}
the core of S.
The obvious criteria for judging whether to try diamond reduction at
all, and of how successful it has been once tried, will be based on the
core.
For since the only nodes we can hope to get rid of are the complement of
the core, we might decide not to bother if there are not enough of these
as a proportion of the whole.
And after carrying out the reduction, we can give a success rating in
terms of the percentage of non-core nodes eliminated.
Experimentation over a wide range of example CSP processes has demonstrated that diamond elimination is a highly effective compression technique, with success ratings usually at or close to 100% on most natural systems. To illustrate how diamond elimination works, consider one of the most hackneyed CSP networks: N one-place buffer processes chained together.
COPYCOPY
... COPY
COPY
Here,
COPY=left?x  right!x
right!x  COPY.
If the underlying type of (the communications on) channel left
(and right) has k members then COPY has k+1
states and the network has
(k+1) N [k+1 to the power N].
Since all of the internal communications (the movement of data from one
COPY to the next) become
COPY.
If the underlying type of (the communications on) channel left
(and right) has k members then COPY has k+1
states and the network has
(k+1) N [k+1 to the power N].
Since all of the internal communications (the movement of data from one
COPY to the next) become
 actions, this is an excellent target for diamond elimination.
And in fact we get 100% success: the only nodes retained are those that
are not
actions, this is an excellent target for diamond elimination.
And in fact we get 100% success: the only nodes retained are those that
are not
 -reachable
from any other.
These are the ones in which all of the data is as far to the left as it
can be: there are no empty COPY's to the left of a full one.
If k=1 this means there are now N+1 nodes rather than
2 N [2 to the power N],
and if k=2 it gives
2 N+1 -1 [one less than 2 to the power N+1]
rather than 3 N [3 to the power N].
-reachable
from any other.
These are the ones in which all of the data is as far to the left as it
can be: there are no empty COPY's to the left of a full one.
If k=1 this means there are now N+1 nodes rather than
2 N [2 to the power N],
and if k=2 it gives
2 N+1 -1 [one less than 2 to the power N+1]
rather than 3 N [3 to the power N].
Go to the Next or Previous section, the Detailed Contents, or the FS(E)L Home Page.