Go to the Next or Previous section, the Detailed Contents, or the FS(E)L Home Page.
1.3 CSP Refinement
The notion of refinement is a particularly useful concept in many forms
of engineering activity.
If we can establish a relation between components of a system which
captures the fact that one satisfies at least the same conditions as
another, then we may replace a worse component by a better one without
degrading the properties of the system.
Obviously the notion of refinement must reflect the properties of a
system which are important: in building bridges it may acceptable to
replace a (weaker) aluminium rivet by a (stronger) iron one, but if
weight is critical, say in an aircraft, this is not a valid refinement.
In describing reactive computer systems, CSP has been found to be a
useful tool.
Refinement relations can be defined for systems described in CSP in
several ways, depending on the semantic model of the language which is
used.
In the untimed versions of CSP, three main forms of refinement are
relevant, corresponding to the three models presented above.
We briefly outline these below, for more information see [Roscoe97].
- Traces refinement
-
The coarsest commonly used relationship is based on the sequences of
events which a process can perform (the traces of the process).
A process Q is a traces refinement of another, P, if all
the possible sequences of communications which Q can do are also
possible for P.
This relationship is written
P
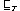 Q.
If we consider P to be a specification which determines possible
safe states of a system, then we can think of
P
Q.
If we consider P to be a specification which determines possible
safe states of a system, then we can think of
P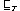 Q
as saying that Q is a safe implementation: no wrong events will
be allowed.
Q
as saying that Q is a safe implementation: no wrong events will
be allowed.
P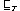 Q
Q
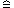 traces(Q)
traces(Q)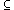 traces(P)
traces(P)
Traces refinement does not allow us to say anything about what will
actually happen, however.
The process STOP, which never performs any events, is a
refinement of any process in this framework, and satisfies any safety
specification.
- Failures refinement
-
A finer distinction between processes can be made by constraining the
events which an implementation is permitted to block as well as those
which it performs.
A failure is a pair (s,X), where s is a trace of
the process and X is a set of events the process can refuse to
perform at that point (and, to add a little more terminology, X
is called a refusal).
Failures refinement
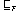 is defined by insisting that the set of all failures of a refining
process are included in those of the refined process.
is defined by insisting that the set of all failures of a refining
process are included in those of the refined process.
P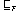 Q
Q
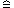 failures(Q)
failures(Q)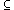 failures(P)
failures(P)
A state of a process is deadlocked if it can refuse to do
every event, and STOP is the simplest deadlocked process.
Deadlock is also commonly introduced when parallel processes do not
succeed in synchronising on the same event.
- Failures-Divergences refinement
-
The failures model does not allow us to easily detect one important
class of states: those after which the process might livelock
(i.e., perform an infinite sequence of internal actions) and so
may never subsequently engage in a visible event.
So, a semantic model more thorough (in this respect) than the failures
model is desirable.
The failures-divergences model meets this requirement by adding the
concept of divergences.
The divergences of a process are the set of traces after which the
process may livelock.
This gives two major enhancements: we may analyse systems which have the
potential to never perform another visible event and assert this does
not occur in the situations being considered; and we may also use
divergence in the specification to describe "don't care" situations.
The relation
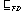 is defined as follows:
is defined as follows:
P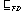 Q Q
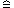
|
failures(Q)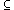 failures(P) failures(P)
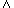
|
|
|
divergences(Q)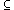 divergences(P) divergences(P)
|
Formally, after a divergence we consider a process to be acting
chaotically and able to do or refuse anything.
This means that processes are considered to be identical after they have
diverged.
Naturally, for divergence-free processes, which include the vast
majority of practical systems,
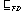 is equivalent to
is equivalent to
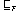
As implied by the name of FDR, we consider
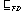 to be the most
important of these three.
We will generally abbreviate
to be the most
important of these three.
We will generally abbreviate
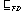 by
by
 .
The failures-divergence model, and its corresponding notion of
refinement, are usually taken as the standard model of CSP.
.
The failures-divergence model, and its corresponding notion of
refinement, are usually taken as the standard model of CSP.
All three of these forms of refinement are supported in FDR.
We would normally expect them to be used in the following contexts:
-
Traces refinement is used for proving safety properties.
-
Failures-divergence refinement is used for proving safety, liveness and
combination properties, and also for establishing refinement and
equality relations between systems.
-
Failures refinement is normally used to prove failures-divergence
refinement for processes that are already known to be divergence-free.
It does have other uses, but these are somewhat more sophisticated.
See the file `abp.csp' in the FDR `demo' directory
for some discussion of this issue.
The following sections illustrate how refinement might be used (by
working through a simple example) and explain how the FDR tool can
check refinement in an automated way.
Go to the Next or Previous section, the Detailed Contents, or the FS(E)L Home Page.
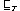 Q.
If we consider P to be a specification which determines possible
safe states of a system, then we can think of
P
Q.
If we consider P to be a specification which determines possible
safe states of a system, then we can think of
P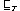 Q
as saying that Q is a safe implementation: no wrong events will
be allowed.
Q
as saying that Q is a safe implementation: no wrong events will
be allowed.
Q
traces(Q)
traces(P)
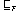 is defined by insisting that the set of all failures of a refining
process are included in those of the refined process.
is defined by insisting that the set of all failures of a refining
process are included in those of the refined process.
Q
failures(Q)
failures(P)
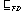 is defined as follows:
is defined as follows:
Q
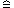
failures(P)
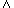
divergences(P)
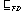 is equivalent to
is equivalent to
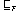
 .
The failures-divergence model, and its corresponding notion of
refinement, are usually taken as the standard model of CSP.
.
The failures-divergence model, and its corresponding notion of
refinement, are usually taken as the standard model of CSP.