Go to the Next or Previous section, the Detailed Contents, or the FS(E)L Home Page.
5.1.3 Hiding and safety properties
If the underlying datatype T of the COPY processes is
large, then chaining N of them together will lead to unmanageably
large state-spaces whatever sort of compression is applied to the entire
system.
Suppose x is one member of the type T; an obviously
desirable (and true) property of the COPY chain is that the
number of x's input on channel left is always greater than
or equal to the number output on right, but no greater than the
latter plus N.
Since the truth or falsity of this property is unaffected by the
system's communications in the rest of its alphabet,
{left.y,right.y |
y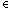
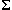 \ {x}},
we can hide this set and build the network up a process at a time from
left to right.
At the intermediate stages you have to leave the right-hand
communications unhidden (because these still have to be synchronised
with processes yet to be built in) but nevertheless, in the traces
model, the state space of the intermediate stages grows more slowly with
n than without the hiding.
In fact, with n COPY processes the hidden version
compresses to exactly
2 n [2 to the power n]
states whatever the size of T (assuming that this is at least
2).
\ {x}},
we can hide this set and build the network up a process at a time from
left to right.
At the intermediate stages you have to leave the right-hand
communications unhidden (because these still have to be synchronised
with processes yet to be built in) but nevertheless, in the traces
model, the state space of the intermediate stages grows more slowly with
n than without the hiding.
In fact, with n COPY processes the hidden version
compresses to exactly
2 n [2 to the power n]
states whatever the size of T (assuming that this is at least
2).
If the (albeit slower) exponential growth of states even after hiding
and compressing the actual system is unacceptable, there is one further
option: find a network with either less states, or better compression
behaviour, that the actual one refines, but which can still be shown to
satisfy the specification.
In the example above this is easy: simply replace COPY with
Cx=( P
P 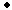 left.x
left.x  right.x
right.x  P)
P)
 CHAOS(
CHAOS(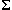 \
{left.x,right.x})
\
{left.x,right.x})
the process which acts like a reliable one-place buffer for the value
x, but can input and output as it chooses on other members of
T (for the definition of CHAOS, see A.4 Processes).
It is easy to show that COPY refines this, and a chain of
n
Cx's
compresses to n+1 states (even without hiding irrelevant external
communications).
The methods discussed in this section can be used to prove properties
about the reliability of communications between a given pair of nodes in
a complex environment, and similar cases where the full complexity of
the operation of a system is irrelevant to why a particular property is
true.
Go to the Next or Previous section, the Detailed Contents, or the FS(E)L Home Page.
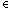
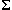 \ {x}},
we can hide this set and build the network up a process at a time from
left to right.
At the intermediate stages you have to leave the right-hand
communications unhidden (because these still have to be synchronised
with processes yet to be built in) but nevertheless, in the traces
model, the state space of the intermediate stages grows more slowly with
n than without the hiding.
In fact, with n COPY processes the hidden version
compresses to exactly
2 n [2 to the power n]
states whatever the size of T (assuming that this is at least
2).
\ {x}},
we can hide this set and build the network up a process at a time from
left to right.
At the intermediate stages you have to leave the right-hand
communications unhidden (because these still have to be synchronised
with processes yet to be built in) but nevertheless, in the traces
model, the state space of the intermediate stages grows more slowly with
n than without the hiding.
In fact, with n COPY processes the hidden version
compresses to exactly
2 n [2 to the power n]
states whatever the size of T (assuming that this is at least
2).
 P
P 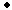 left.x
left.x  right.x
right.x  CHAOS(
CHAOS(